
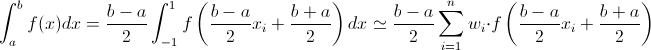
Additionally, a new lowest-order (piecewise constant) preconditioner is developed for high-order interior penalty discontinuous Galerkin (DG) discretizations, for which spectral equivalence results and convergence proofs for algebraic multigrid methods are provided.
#Abscissa quadrature point full#
This spectral equivalence, coupled with algebraic multigrid methods constructed using the low-order discretization, results in highly scalable matrix-free preconditioners for high-order finite element problems in the full de Rham complex. This theory covers diffusion problems in $H^1$, $H()$, and is based on combining a low-order discretization posed on a refined mesh with a high-order basis for N\'ed\'elec and Raviart-Thomas elements that makes use of the concept of polynomial histopolation (polynomial fitting using prescribed mean values over certain regions). Roots(n) being n and weights for some other (Gaussian) quadrature.In this paper we present a unified framework for constructing spectrally equivalent low-order-refined discretizations for the high-order finite element de Rham complex. Order with positive weights for the abscissa x give (y, wy) = _init_ ( mesg=None, res=None, err=None ) ¶ _1d.quadrature. IntegrationError ( mesg=None, res=None, err=None ) ¶Įrror during integration. Return the function g(y) which, when integrated over PowerDecay ( x, n, x0=0 ) ¶īases: _1d.quadrature.Decay X._init_(.) initializes x see help(type(x)) for signature class _1d.quadrature. Returns self, the complex conjugate of any float.Ĭreate a floating-point number from a hexadecimal string. Returns a pair of integers, whose ratio is exactly equal to the original float and with a positive denominator. Represents information about the asymptotic form of indefinite Using a subclass of Decay such as PowerDecay orĮxpDecay to effect a transformation for dealing with these In particular, the nature of the decay at inf can be described by ItĪllows the user to specify properties of the integrand to facilitate Integrate(), which performs a one-dimensional integral. This module provides access to several adaptive quadrature routinesįor performing one-dimensional integrals. Inheritance diagram for _1d.quadrature:Īdaptive quadrature routines for one-dimensional integrals. Return the abscissa and weights for the Gaussian quadrature of Return (res, err) where res is the numerically evaluated Return (res, err) where res is the integral of the function f(x) from a to b and err is an estimate of the absolute error.Īn improved version of integrate.quad that does some argument checking and deals with points properly. Return the weights wx for a quadrature of order at least n >= len(y) for the abscissa x give the n exact quadrature abscissa y and weights wy defining a quadrature of order 2n. Return the list of weights wx for quadratures of increasing Represents information about the asymptotic form of indefinite integrals.


 0 kommentar(er)
0 kommentar(er)
